原文链接：寻找知识 (opens new window)

本系列文章 以非专业的视角介绍零知识相关知识。

And what, Socrates, is the food of the soul? Surely, I said, knowledge is the food of the soul. 苏格拉底，什么是灵魂的食物？我说过，当然是知识。 —— 柏拉图

零知识 vs. 可靠性

许多介绍零知识证明的文章都会提到以下三个性质：

• Completeness -- 完备性
• Soundness -- 可靠性
• Zero-Knowledge -- 零知识

但是少有文章深入解释这个特性背后的深意和洞见。

理解模拟 一文介绍了模拟器这个概念。许多介绍文章也避而不谈模拟，但模拟可以说是安全协议中核心的核心，因为它是定义安全性的重要武器。

通常，我们定义安全会采用这样一种方式--首先列出一些安全事件，然后说明如果一个系统安全，那么列出来的安全事件都不会发生。

Rather than giving a list of the events that are not allowed to occur, it (the definition of zero-knowledge proof) gives a maximalist simulation condition.

— Boaz Barak

借用密码学家 Boaz Barak 的话，翻译一下，零知识证明并不是通过给出一个不允许发生的事件列表来定义，而是直接给出一个最极致的模拟条件。

所谓模拟条件是指，通过模拟方法来实现一个理想世界，使之与现实世界不可区分。而由于理想世界不存在知识，所以可推导出结论：现实世界满足零知识。

我们继续分析下一个交互系统（安全协议）的三个性质：完备性、可靠性与零知识。

可靠性（Soundness）：Alice 在没有知识的情况下不能通过 Bob 的验证。
完备性（Completeness）：Alice 在有知识的情况下可以通过 Bob 的验证。
零知识（Zero-knowledge）：Alice 在交互的过程中不会泄露关于知识的任何信息。

可以看到可靠性和完备性具有对称性--可靠性保证了恶意的 Alice 一定失败，而完备性保证了诚实的 Alice 一定成功。

完备性比较容易证明。只要 Alice 诚实，Bob 也诚实，那么皆大欢喜。这好比，写好一段代码，喂了一个测试用例，跑完通过收工。

可靠性应该如何定义？这个可靠性的逆否命题是：（在现实世界中）如果 Alice 能通过 Bob 的验证，那么 Alice 一定有知识。或者说：Alice 知道那个秘密！

下面的问题是如何证明 Alice 知道一个秘密？

这好像也很难。假如我们需要证明机器知道一个秘密，最简单的办法就是在机器的硬盘或者内存找到这个秘密，但是这样暴露了秘密。如果这台机器是黑盒子呢？或者是 Alice 呢？我们没有读心术，猜不到她心里的那个秘密。

如何定义To Know？

零知识保证了验证者 Bob 没有（计算）能力来把和知识有关的信息抽取出来。不能抽取的知识不代表不存在。可靠性保证了知识的存在性。

只有在存在知识的前提下，保证零知识才有意义

本文将探讨可靠性和To Know。

为了进一步分析知识，接下来首先介绍一个非常简洁，用途广泛的零知识证明系统 -- Schnorr 协议。这个协议代表了一大类的安全协议--所谓的 Σ-协议。而且 Schnorr 协议扩展也是 零知识数据交换协议 zkPoD (opens new window) 的核心技术之一。

简洁的 Schnorr 协议

Alice 拥有一个秘密数字 a，可以把这个数字想象成私钥，可映射到椭圆曲线群上的一个点 a*G。这个点当做公钥。

请注意映射这个词。这里先简要介绍同态这个概念。椭圆曲线群有限域之间存在着一种同态映射关系。有限域用 Zq这个符号表示，其中素数 q 指有限域的大小，是从 0, 1, 2, ..., q-1 这样一个整数集合。在一条椭圆曲线上，通过一个基点 G，可以产生一个循环群，标记为 0G, G, 2G, ..., (q-1)*G，正好是数量为 q 个曲线点的集合。任意两个曲线点可以进行一种特殊的二元运算，G + G = 2G，2G + 3G = 5G，看起来这个二元运算和加法类似，满足交换律和结合律。于是我们就用 + 这个符号来表示。这个群称为循环群是因为把群的最后一个元素 (q-1)*G，再加上一个 G 就回卷到群的第一个元素 0G。

给定任意一个有限域上的整数 r，可以在循环群找到一个对应的点 r*G。但是通过 r*G 反过来计算 r 是很困难的，被称为离散对数难题 [2]。

也就是说，如果任意给一个椭圆曲线循环群上的点 R，计算出有限域的哪一个整数对应 R 是很难的。如果有限域足够大，比如说 256 比特，姑且可以认为这个反向计算是不可能做到的。

Schnorr 协议充分利用了有限域和循环群之间单向映射，实现了最简单的零知识证明安全协议：Alice 向 Bob 证明她拥有 PK 对应的私钥 sk。

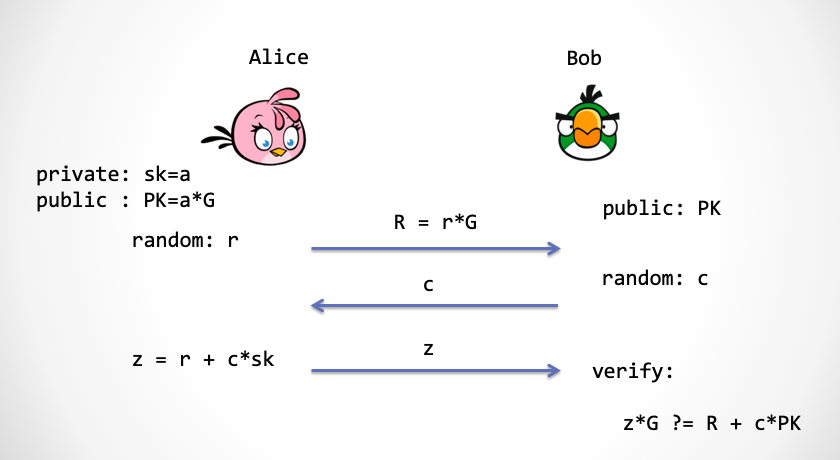
1. 为了保证零知识，Alice 需要先产生一个随机数 r，这个随机数的用途是用来保护私钥无法被 Bob 抽取出来。这个随机数也需要映射到椭圆曲线群上，r*G。
2. Bob 要提供一个随机数 c 进行挑战。
3. Alice 根据挑战数计算 z = r + a * c，同时把 z发给 Bob。Bob 通过下面的式子进行检验：

   z*G ?= R + c*PK = rG + c*(aG)
   

可以看到 Bob 在第 3 步同态地检验 z 的计算过程。如果这个式子成立，那么就能证明 Alice 确实有私钥 a。何解？

z 的计算和验证过程很有趣，有几个关键技巧：

1. 首先 Bob 必须给出一个随机挑战数，然后 Bob 在椭圆曲线上同态地检查 z 。如果我们把挑战数 c 看成是一个未知数，那么 r+a*c=z 可以看成是一个一元一次方程，其中 r 与 a 是方程系数。请注意在 c 未知的前提下，如果 r + a*x = r' + a'*x 要成立，那么根据 Schwatz-Zippel 定理 [3]，极大概率上 r=r'，a=a' 都成立。也就是说，Alice 在 c 未知的前提下，想找到另一对不同的 r',a' 来计算 z 骗过 Bob 是几乎不可能的。这个随机挑战数 c 限制了 r 和 a。虽然 Bob 随机选了一个数，但是由于 Alice 事先不知道，所以 Alice 不得不使用私钥 a 来计算 z。这里的关键：c 必须是个随机数。
2. Bob 的验证在椭圆曲线群上完成。Bob 不知道 r，但是他知道 r 映射到曲线上的点 R。Bob 也不知道 a，但是他知道 a 映射到曲线群上的点 PK，即 a*G。通过同态映射与 Schwatz-Zippel 定理，Bob 可以校验 z 的计算过程是否正确，从而知道 Alice 确实是通过 r 和 a 计算得出的 z，但是又不暴露 r 与 a 的值。
3. 协议第 1 步产生的随机数 r 保证了 a 的保密性。任何一个秘密和一个符合一致性分布的随机数相加的和仍然符合一致性分布。

证明零知识

我们这里看一下 Schnorr 协议如何证明一个弱一些的零知识性质——SHVZK：

这里我们证明的仅仅是 Special Honest Verifier Zero-Knowledge（SHVZK）。SHVZK 要求协议中的 Bob 必须按常理出牌，比如他必须按协议约定，在第 2 步时，去传送带上取一个新鲜的随机数，并且立即使用。通常意义上的零知识不会对 Bob 做任何要求，所以说这里是一个弱一些的性质。虽然目前 Schnorr 协议不能证明完全的零知识，但经过添加一些协议步骤，就可以达到完全零知识的目的。细节这里不展开，有兴趣的读者请参考文献 [4]。以后我们在讨论 Fiat-Shamir 变换时，还会再次讨论这个问题。

首先模拟器模拟一个理想世界--在理想世界模拟出一个 Zlice 和 Bob 对话。Zlice 没有 Schnorr 协议中的知识 sk，而 Bob 是有公钥 PK的。请大家看下图，Bob 需要在 Schnorr 协议的第 2 步出示一个随机数 c，这里有个额外的要求，就是 Bob 只能诚实地从一个外部随机数传送带拿一个随机数，每一个随机数都必须是事先抛 k 次硬币产生的一个 2^k 范围内的一次性分布随机数。Bob 不能采用任何其他方式产生随机数，这就是为何我们要求 Bob 是诚实的。

下面演示 Zlice 如何骗过 Bob：

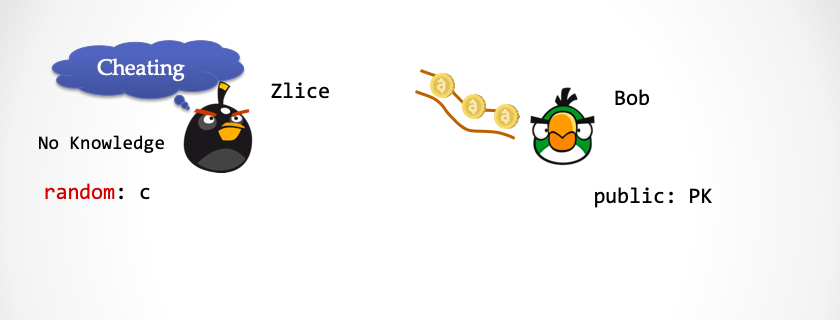
序幕：请注意 Zlice 没有关于sk的知识，这时 Bob 的随机数传送带上已经预先放置了一些随机数。

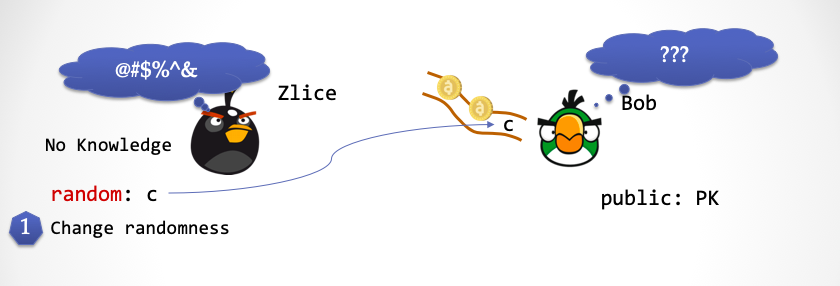
1. Zlice 产生一个一致性分布的随机数 c，并且利用一个新的超能力，用刚刚产生的随机数 c 替换掉 Bob 的随机数传送带上第一个随机数。这时候，Bob 无法察觉。

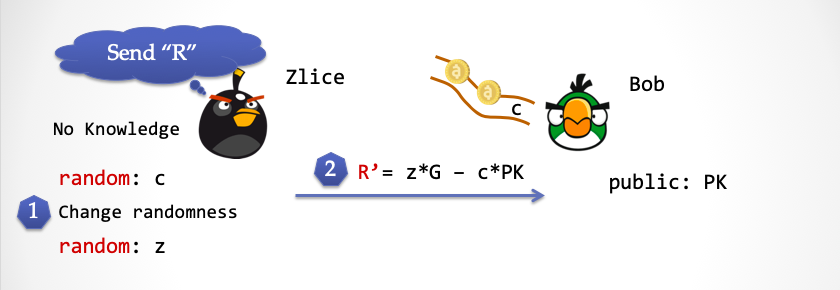
2. Zlice 再次产生一个随机数 z，然后计算 R'=z*G - c*PK，并将 R'发送给 Bob。

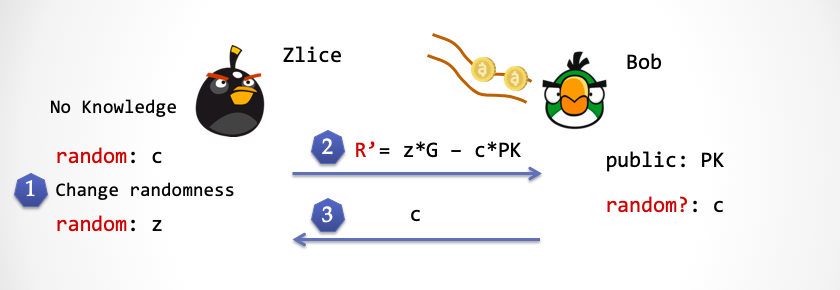
3. Bob 从随机数传送带上取得 c，并且将 c 发送给 Zlice。请注意这个c 正好就是第 1 步 Zlice 产生的 c。

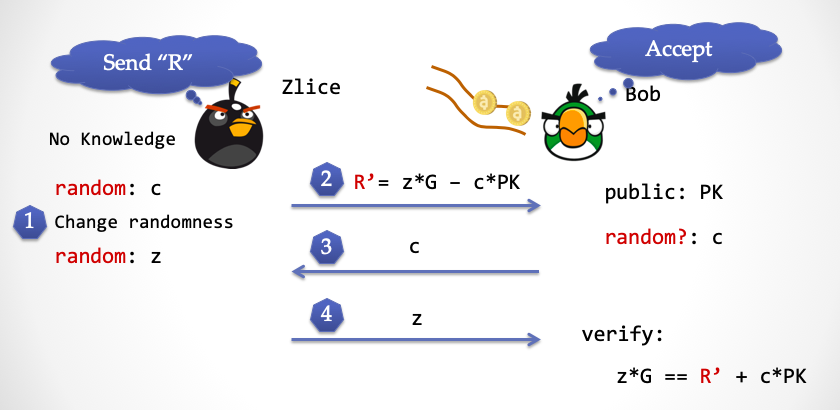
4. Zlice 将第三步产生的随机数 z 发送给 Bob，Bob 按照 Schnorr 协议的验证公式进行验证，大家可以检查下，这个公式完美成立。

再对比下现实世界的 Schnorr 协议，发现在两个世界中 Bob 都能通过验证。

但区别是：

• 理想世界中，Zlice 没有 sk；而在现实世界中，Alice 有 sk
• 理想世界中，z 是一个随机数，没有涉及 sk；而在现实世界中，z 的计算过程里面包含 sk
• 理想世界中，Zlice 使用超能力替换了 Bob 的随机数；而在现实世界中，Alice 看不到 Bob 的随机数传送带，也无法更改传送带上的数字

这里请大家思考下：Schnorr 协议中，Bob 在第 2 步发挑战数能不能和第一步对调顺序？也就是说 Bob 能不能先发挑战数，然后 Alice 再发送 R = r*G。

（两分钟后 ......）

答案是不能。

如果 Alice 能提前知道随机数，那么（现实世界中的）Alice 就可以按照模拟器 Zlice 做法来欺骗 Bob。

再遇模拟器

其实，可靠性和零知识这两个性质在另一个维度上也是存在着一种对称性。可靠性保证恶意的 Alice 一定失败，零知识保证恶意的 Bob （窃取知识）一定不会成功。有趣地是，这种对称性将体现在模拟出来的理想世界中。

我们分析下可靠性这个定义：Alice 没有知识 导致 Bob 验证失败。它的逆否命题为：Bob 验证成功 导致 Alice 一定有知识。

我们再次求助模拟器，让他在可以发挥超能力的理想世界中，去检验 Alice 的知识。

再次，请大家设想在平行宇宙中，有两个世界：理想世界和现实世界。理想世界有趣的地方在于它是模拟器模拟出来的，同时模拟器可以在理想世界放入带有超能力的 NPC。这次把 Alice 的两个分身同时放入理想世界与现实世界。

假设你扮演 Bob 的角色，想知道对话的 Alice 是否真的是可靠的。于是把你放入理想世界，借助一个具有超能力的 NPC，你可以把对面的 Alice 的知识抽取出来。

什么鬼？我们不是刚刚证明过：协议是零知识的吗？零知识就意味着 Bob 抽取不出任何的知识碎片。这里敲黑板：零知识是对于现实世界而言的。我们现在正在讨论的是神奇的理想世界。

重申一遍：在理想世界中，你可以借助一个有超能力的 NPC 来抽取 Alice 的知识，从而保证现实世界的 Alice 无法作弊。可以想象一下，一个作弊的 Alice，她肯定没有知识，没有知识也就不可能在理想世界让 NPC 抽取到任何东西。

然而现实世界没有可借助的 NPC，当然也就看不到 Alice 的知识，也就不会和零知识性质冲突。因为两个世界发生的事件是不可区分的，我们可以得到这样的结论：在现实世界中，Alice 一定是存在知识的。

整理一下思路：如何证明在一个交互会话中 Alice 不能作弊呢？我们需要为这个交互会话定义一个模拟算法，该算法可以模拟出一个理想世界，其中有一个特殊的角色叫做抽取器(Extractor)，也就是前面说的 NPC，它能够使用超能力来抽取Alice 的知识，但是让对方无所察觉。

注意：超能力是必不可少的！这一点在 理解模拟 有解释：如果模拟器在没有超能力的情况下具备作弊能力，那相当于证明了协议不可靠（Unsoudness）。同样地，如果抽取器在没有超能力的情况下具备抽取信息能力，那相当于证明了协议不零知（Not-zero-knowledge）。

最后一点，超能力是什么？这个要取决于具体交互系统的证明。接下来从刚刚讲过的 Schnorr 协议切入。

知识证明

我们来证明一下 Schnorr 协议的可靠性，看看这个超能力 NPC 如何在理想世界把 Alice 私钥抽取出来。而这个超能力，仍然是时间倒流。

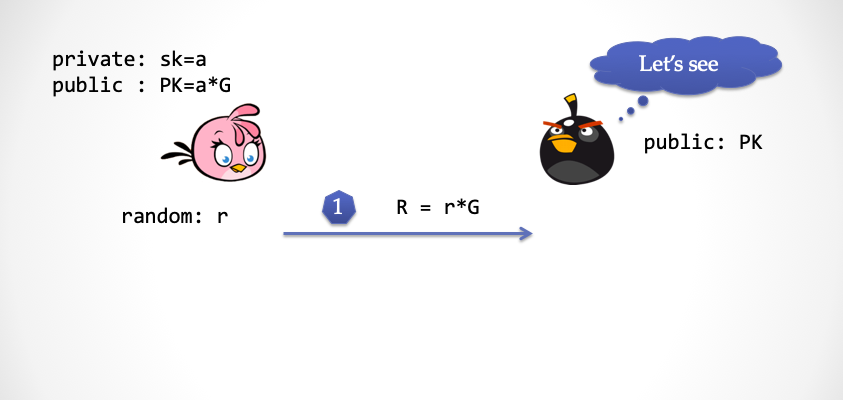
1. Alice 选择一个随机数 r，并且计算 R=r*G，并将 R 发给抽取器

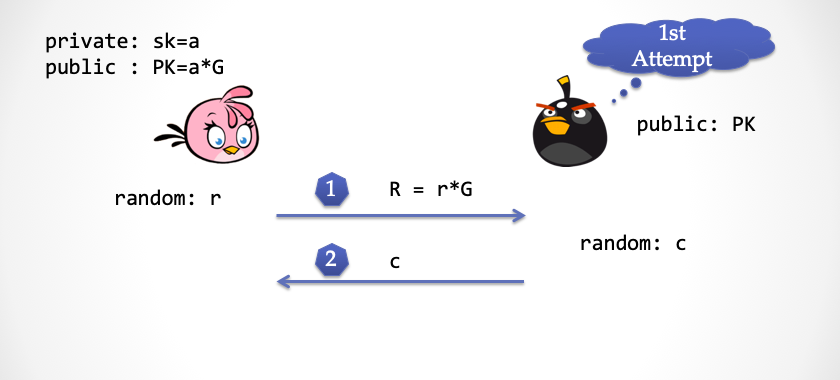
2. 抽取器也选择一个随机的挑战数 c，并且发给 Alice

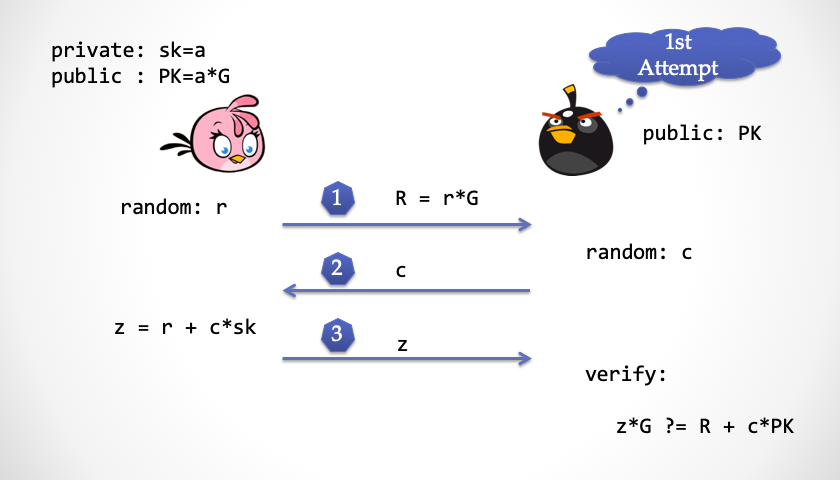
3. Alice 计算并且回应 z，然后抽取器检查 z 是否正确

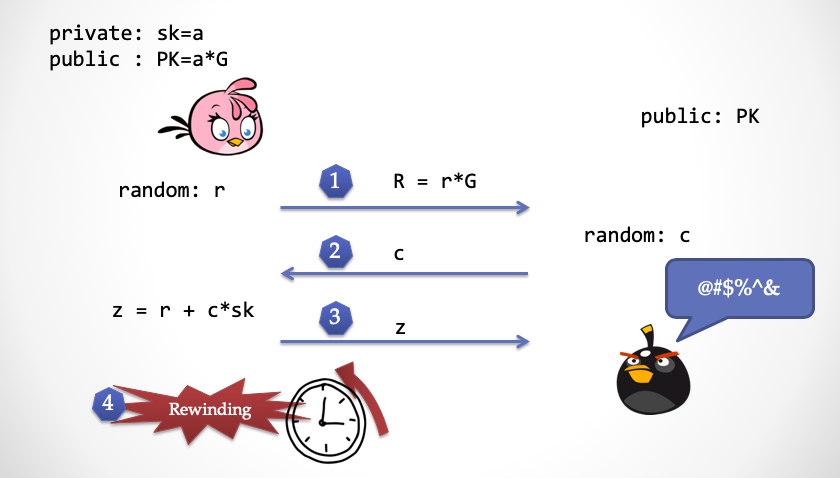
4. 抽取器发现 z 没有问题之后，发动超能力，将时间倒回第 2 步之前

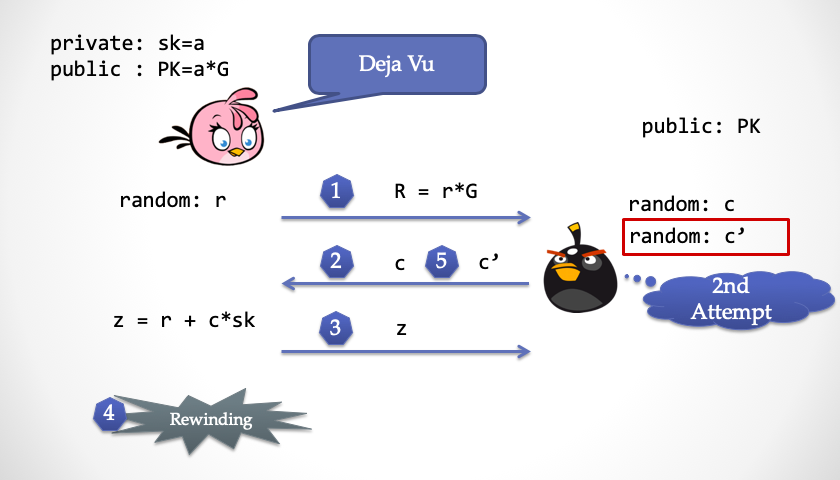
5. 抽取器再次发送一个不同的随机挑战数 c' 给 Alice，这时 Alice 回到第 2 步，会有一种似曾相识的感觉，但是无法感知到时间倒回这个事实

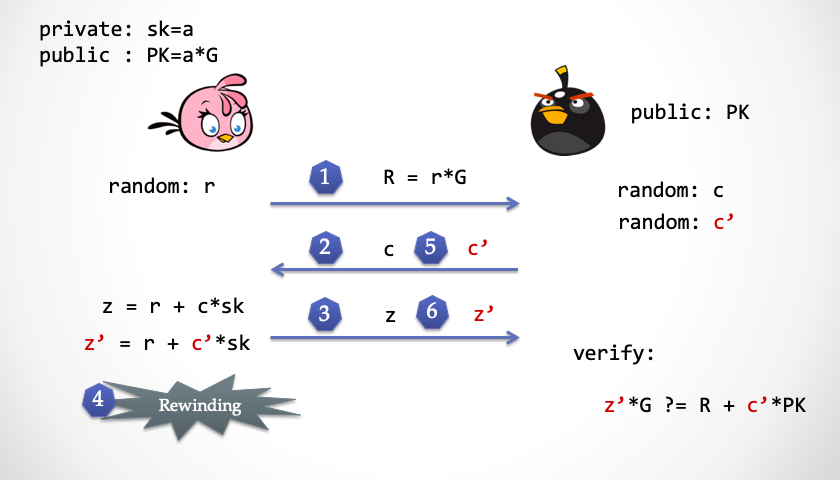
6. Alice 再次计算了 z'，然后发给抽取器检查

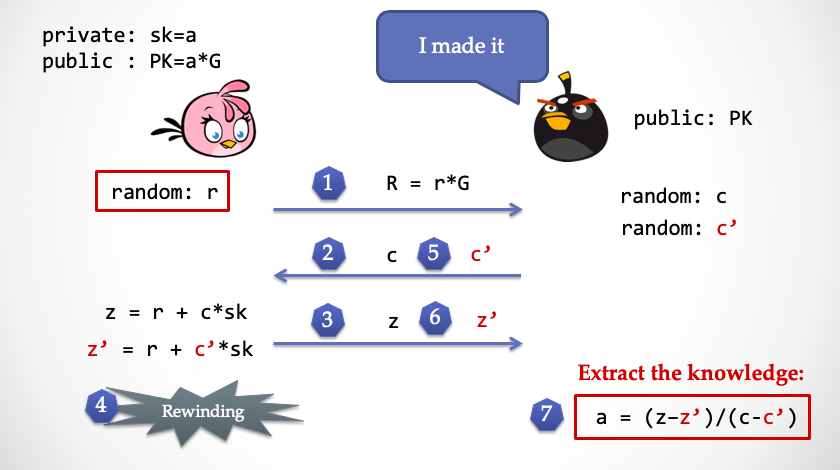
7. 这时候抽取器有了 z 和 z'，就可以直接推算出 Alice 所拥有的私钥 a，达成知识抽取

到这里，可靠性就基本证明完了。大家是不是对可靠性和零知性的对称性有点感觉了？

总结一下：抽取器在理想世界通过时间倒流的超能力，把 Alice 的知识完整地抽取出来，保证了一个没有知识的 Alice 是无法让抽取器达成目标，从而证明了可靠性。

注：并不是所有的可靠性都必须要求存在抽取器算法。采用抽取器来证明可靠性的证明系统被称为Proof of Knowledge。

解读 ECDSA 签名攻击

在区块链系统中到处可见的 ECDSA 签名方案也是一个朴素的零知识证明系统。椭圆曲线数字签名方案 ECDSA 与 Schnorr 协议非常接近，基于 Schnorr 协议的签名方案发表在 1991年的《密码学杂志》[5] 上。1991年，正值美国国家标准局（NIST）选择数字签名算法，优雅的 Schnorr 签名方案居然被申请了专利，因此 NIST 提出了另一套签名方案 DSA（Digital Signature Algorithm）。随后这个方案支持了椭圆曲线，于是被称为 ECDSA。中本聪在构思比特币时，选择了 ECDSA 作为签名算法，但是曲线并没有选择 NIST 标准推荐的椭圆曲线 -- secp256-r1，而是 secp256-k1。因为江湖传言，NIST 可能在椭圆曲线参数选择上做了手脚，导致某些机构可以用不为人知的办法求解离散对数难题，从而在现实世界具备超能力。有不少人在怀疑，也许当年中本聪在设计比特币时，也有这种考虑，故意选择了 secp256-k1 这样一条貌似安全性稍弱的曲线。

我们拆解下 ECDSA 签名，用交互的方式定义一个类似 ECDSA 的认证方案，交互见下图。

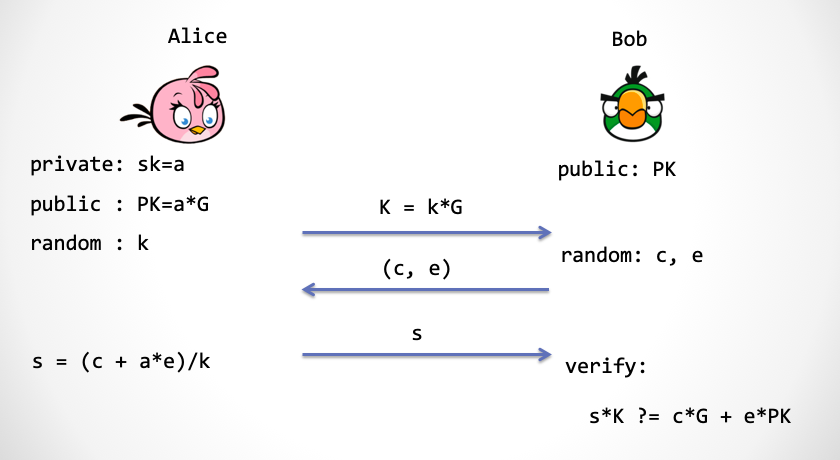
1. Alice 仍然是选择一个随机数 k，并将 k 映射到椭圆曲线上，得到点 K ，然后发送给 Bob
2. Bob 需要产生两个随机数，c 和 e，然后交给 Alice
3. Alice 计算 s，并且发送给 Bob，他来验证 s 的计算过程是否正确

对熟悉 ECDSA 签名方案的读者，这里略作解释：Bob 产生的 c 对应被签消息的 Hash 值 Hash(m)，而 e 则是由一个转换函数 F(K)来产生。其中 F(.) 是取椭圆曲线点的 x 坐标经过 (mod q) 得到 [6]。

江湖上流传着一个说法：ECDSA 签名方案有个严重的安全隐患--如果在两次签名使用了同一个随机数，那么签名者的私钥将会暴露出来。其实 Schnorr 签名方案也有同样的问题。

当年 Sony PlayStation 3 的工程师在调用 ECDSA 库函数时，本来应该输入随机数的参数位置上，却传入了一个常数。熟悉密码学的黑客们发现了这个严重的后门。2011 年 1 月，神奇小子 Geohot 公开发布了 Sony PS3 的主私钥，这意味着任何用户都可以轻松拿到游戏机的 root 权限。Sony 随后大为光火....... （后续故事大家可以上网搜）

如果 Alice 在两次交互过程中使用了同一个 K，那么 Bob 可以通过发送两个不同的 c 和 c' 来得到 s 和 s'，然后通过下面的公式算出私钥 a：

k = (c - c')/(s - s')
a = (k * s - c)/e

那么我们应该怎么看待这个安全后门呢？大家想想看，这个安全后门和前面证明过的 Schnorr 协议的可靠性证明几乎一模一样！这个算法正是 ECDSA 认证协议的可靠性证明中的抽取器算法。只不过在可靠性证明中，为了让 Alice 使用同一个随机数 k 来认证两次，抽取器需要利用时间倒流的超能力。

但是在 Sony PS3 系统中，随机数被不明所以的工程师写成了一个固定不变的值，这样相当于直接赋予了黑客超能力，而这是在现实世界中。或者说，黑客在不需要时间倒流的情况下就能实现抽取器。

提醒下，不仅仅是随机数不能重复的问题。而是随机数必须是具有密码学安全强度的随机数。

设想下，如果随机数 r 是通过一个利用线性同余原理的伪随机数生成器产生，虽然 r 的值一直在变化，但是仍然不能阻止知识抽取。假设线性同余算法为 r2= d*r1 + e (mod m)，还回到 Schnorr 协议的第 3 步：

1: z1 = r1 + c1*a
2: z2 = r2 + c2*a

如果攻击者让 Alice 连续做两次签名，那么将 r2 代入 r1 之后，就出现了两个线性方程求解两个未知数 (r1, a) 的情况，z1, z2, c1, c2, d, e 对于攻击者是已知的，这个方程组只用初中数学知识就可以求解。

请注意：这并不是 Schnorr 协议（或 ECDSA 协议）的设计缺陷。恰恰相反，这是 Schnorr 协议设计比较精巧的地方，它从原理上保证了协议的可靠性。类似技巧在密码学协议中频繁出现，达到一目了然的简洁。但是也不得不说，如果不清楚协议的内在机制，尤其是区分不清楚理想世界与现实世界，使用者很容易引入各种花式的安全漏洞。

作为一个能写出可靠软件的靠谱码农，我们需要了解哪些？彻底理解安全协议的设计机制当然是最好的，但是绝大多数情况下是非常耗费精力的。一般来说，把各种密码学工具当做黑盒来用可能是不够的，我们最好还能了解下：

1. 安全定义是什么？
2. 安全假设到底是什么？
3. 理想世界的超能力到底是什么？

脑洞：我们生活在模拟世界中吗

第一次读懂模拟器时，我第一时间想到的是电影《黑客帝国》。我们生活所在现实世界也许是某一个模拟器模拟出来的理想世界，看到、听到以及感知到的一切都是被模拟出来的。在现实世界里，我们活在一个母体中，然而并不能意识到这一点。

早在春秋战国时期，庄子也在思考类似的问题：

昔者庄周梦为胡蝶，栩栩然胡蝶也，自喻适志与，不知周也。俄然觉，则蘧蘧然周也。不知周之梦为胡蝶与，胡蝶之梦为周与？周与胡蝶，则必有分矣。此之谓物化。——《庄子·齐物论》

通俗地解释下：庄子有一天睡着了，梦见自己变成了一只蝴蝶，翩翩起舞，醒来之后发现自己还是庄子。在梦中，蝴蝶并不知道自己是庄子。于是庄子沉思到底是他梦中变成了蝴蝶，还是蝴蝶梦中变成了庄子呢？如果梦境足够真实，......

缸中之脑是美国哲学家 Gilbert Harman 提出的这样一个想法：一个人的大脑可以被放入一个容器里面，然后插上电线，通过模拟各种电信号输入，使得大脑以为自己活在真实世界。

这个想法源自哲学家笛卡尔的《第一哲学沉思集》[7]，在书中他论证我们应该怀疑一切，需要逐一检验所有人类的知识--数学、几何以及感知到的世界。然而他发现除了我思故我在之外，所有的知识都可能不靠谱，因为我们的大脑很可能被一个具有超能力的恶魔所欺骗。

2003 年牛津大学的哲学教授 Nick Bostrom 郑重其事地写了一篇论文《我们生活在计算机模拟世界中吗？》[8]。认为以下三个事实中，至少有一个成立：

1. 人类文明彻底灭绝。
2. 人类文明已经到达可以完全模拟现实世界的科技水平，但是处于某种原因，没有一个人愿意去创造出一个新的模拟世界，充当上帝的角色。
3. 我们现在的人类文明就生活在一个模拟世界。

硅谷企业家 Elon Musk 在一次公开采访中，谈到我们生活在基础现实世界的概率只有十亿分之一。也就是说，他认为我们生活在一个电脑游戏（模拟世界）中，在模拟世界之外，有一个程序员，他开发并操纵了这个世界，我们每个人都是一个游戏角色（NPC）。

在玩腻越狱 iPhone 和自动驾驶之后，神奇小子 Geohot 在今年三月份的西南偏南大会上做了一个题为Jailbreaking the Simulation的演讲 [9]。他认为：我们被生活在一个模拟世界，所谓的上帝就是外部世界里活蹦乱跳的码农们。他们编程创造了我们的现实世界，可能启动了不止一个世界副本。然而，他们可能也生活在一个外层模拟世界。

如果我们确实生活在模拟世界，或许我们可以在地球的某个地方找到一个后门——Simulation Trapdoor，从而获得模拟器的超能力，抽取出不可思议的秘密知识。

如果我们的世界的确是被程序模拟出来的，这个程序也许会有 Bug。如果有 Bug 存在，说不定我们可以利用这个 Bug 进行越狱，跳出理想世界，到达外面一层的世界，与可爱的码农上帝聊一聊。

这是在开玩笑吗？下面摘自自知乎的一个段子 [10]：

• 问题：如果世界是虚拟的，有哪些实例可以证明？。
• 回答：

1. 为什么宏观上丰富多彩，但是微观的基本粒子却都是一模一样的？这正和图片富多彩，但是像素是一模一样的一回事
2. 为什么光速有上限？因为机器的运行速度有限
3. 为什么会有普朗克常量？因为机器的数据精度有限
4. 为什么微观粒子都是几率云？这是为了避免系统陷入循环而增加的随机扰动
5. 为什么有泡利不相容原理？看来系统采用的数据组织是多维数组
6. 为什么量子计算机运行速度那么快，一瞬间可以尝试所有可能？因为这个本质上是调用了宿主机的接口
7. 为什么会有量子纠缠？这实际上是引用同一个对象的两个指针
8. 为什么会有观察者效应？这显然是lazy updating
9. 为什么时间有开端？系统有启动时间

未完待续

设计一个密码学协议就好像在走钢丝--如果想同时做到零知识和可靠性就意味着既要让协议内容充分随机，又要保证知识能够参与协议的交互。如果协议没有正确设计，亦或没有正确工程实现，系统安全性将会坍塌。比如可能破坏了零知性，导致知识在不经意间泄露；或者破坏了可靠性，导致任何人都能伪造证明。这种安全性远比传统的代码底层机制漏洞来得更加严重，并且更难被发现。严格数学论证似乎是必不可少的。

我们的世界真的是某个三体文明模拟出来的吗？不能排除这个可能性，或许我们需要认真地重新审视自己的各种执念。不过那又怎么样呢？至少自己的思想是真实的。

If you would be a real seeker after truth, it is necessary that at least once in your life you doubt, as far as possible, all things. 如果你是一个真正的真理探求者，在你人生中至少要有一次，尽可能地质疑所有的事情。 -- 笛卡尔

致谢：特别感谢 Shengchao Ding, Jie Zhang，Yu Chen 以及安比实验室小伙伴们(p0n1, even, aphasiayc, Vawheter, yghu, mr)的建议和指正。

参考文献

• [2] Hoffstein, Jeffrey, Jill Pipher, Joseph H. Silverman, and Joseph H. Silverman. An introduction to mathematical cryptography. Vol. 1. New York: springer, 2008.
• [3] Schwartz–Zippel Lemma. Wikipedia. https://en.wikipedia.org/wiki/Schwartz%E2%80%93Zippel_lemma
• [4] Damgård, Ivan. "On Σ-protocols." Lecture Notes, University of Aarhus, Department for Computer Science (2002).
• [5] Schnorr, Claus-Peter. "Efficient signature generation by smart cards." Journal of cryptology 4.3 (1991): 161-174.
• [6] Brown, Daniel RL. "Generic groups, collision resistance, and ECDSA." Designs, Codes and Cryptography 35.1 (2005): 119-152.
• [7] 笛卡儿, 徐陶. 第一哲学沉思集. 九州出版社; 2008.
• [8] Bostrom, Nick. "Are we living in a computer simulation?." The Philosophical Quarterly 53.211 (2003): 243-255.
• [9] Nick Statt. "Comma.ai founder George Hotz wants to free humanity from the AI simulation". Mar 9, 2019. https://www.theverge.com/2019/3/9/18258030/george-hotz-ai-simulation-jailbreaking-reality-sxsw-2019
• [10] doing@知乎. "如果世界是虚拟的，有哪些实例可以证明？". 2017. https://www.zhihu.com/question/34642204/answer/156671701